ATAC-seq data analysis: from FASTQ to peaks

Posted on | In , | | Views:
| 29k | 0:26

The content were compiled from multiple resources on the internet (forum, papers, workshop etc.). I could not indicate all the sources, but I want to thank them for sharing experiences/knowledge/code.

ATAC-seq overview

ATAC-seq (Assay for Transposase-Accessible Chromatin with high-throughput sequencing) is a method for determining chromatin accessibility across the genome. It utilizes a hyperactive Tn5 transposase to insert sequencing adapters into open chromatin regions.

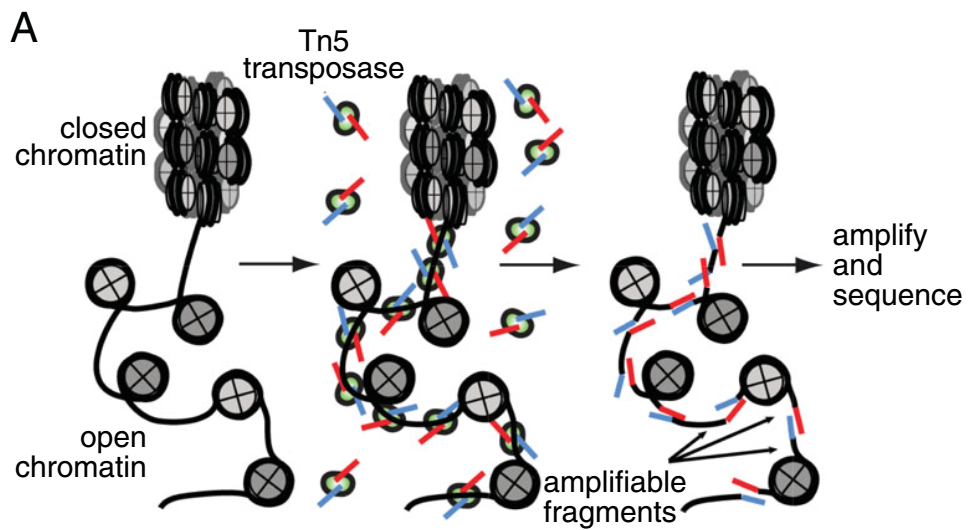
ATAC-seq overview (Buenrostro et al., 2015).

And the peaks look like the following figure.

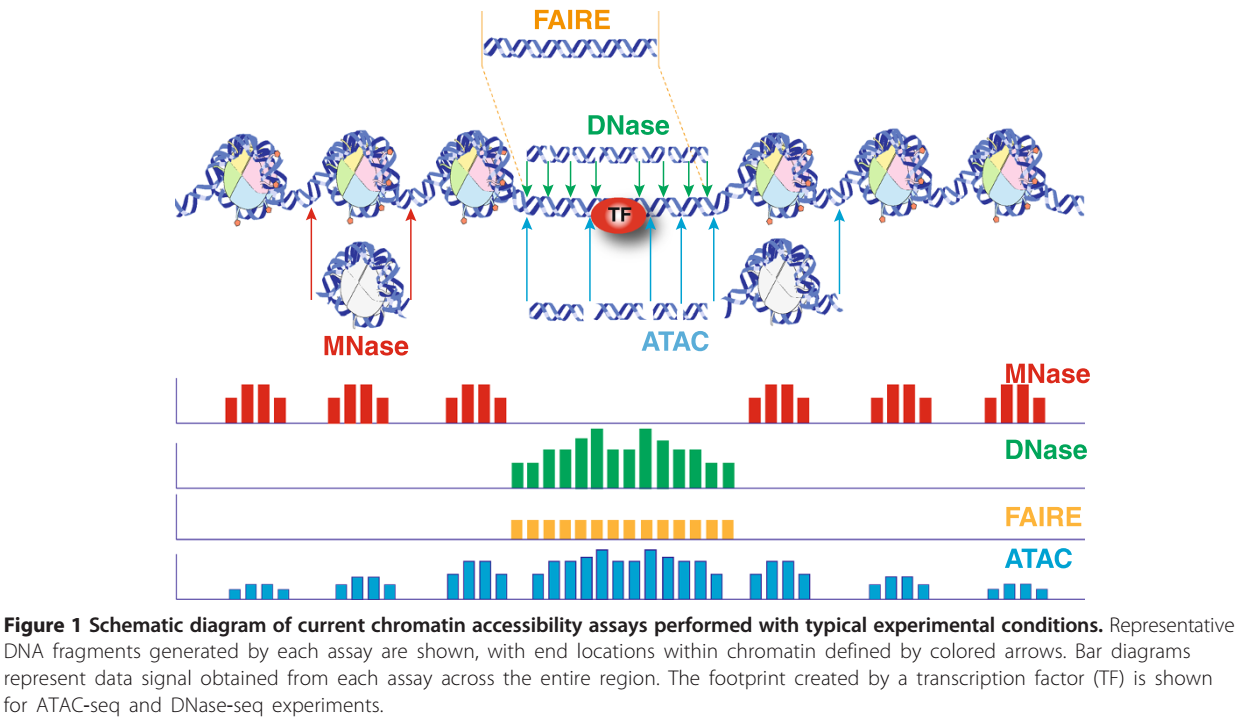
ATAC-seq peaks (Tsompana and Buck, 2014)

And ATAC-seq can be used to:

  • generate epigenomic profiles
  • map accessible chromatin across tissues or conditions
  • retrieve nucleosome positions
  • identify important transcription factors
  • generate occupancy profiles of TFs (footprinting)

Experimental design

See Buenrostro et al., 2015, ENCODE - ATAC-seq Data Standards and Prototype Processing Pipeline, and Harvard FAS Informatics - ATAC-seq Guidelines for details.

  • two or more biological replicates
  • each replicate has 25 million non-duplicate, non-mitochondrial aligned reads for single-end sequencing and 50 million for paired-ended sequencing
  • typically, no need for “input”
  • use as few PCR cycles as possible when constructing the library
  • paired-end sequencing is preferred

Data analysis

Several useful pipelines.

The following pipeline includes several common analysis in ATAC-seq setting, from data trimming to peak calling. Some steps are optional, like merging BAMs.

Quality control

Just like analyzing other NGS data, quality control is needed for raw FASTQ, and there are many programs avaliable, such as Trimmomatic and Trim Galore.

Alignment and filter

The next step is to align reads to a reference genome. Two popular aligners are BWA and Bowtie2. I will use Bowtie2 (since it was used in many tutorals and papers).

1
2
3
4
5
# better alignment results are frequently achieved with --very-sensitive
# use -X 2000 to allow larger fragment size (default is 500)
bowtie2 --very-sensitive -X 2000 -x $Bowtie2Index -1 ${sample}*_1.fq.gz -2 ${sample}*_2.fq.gz \
  -p $PPN 2> $${sample}.bowtie2.log | $path2samtools sort -@ $PPN -O bam -o ${sample}.sorted.bam
$path2samtools index -@ $PPN $WORKDIR/bowtie2/${sample}.sorted.bam

Then, the alignment results should be filtered.

Mitochondrial reads

Ref: Harvard FAS Informatics - ATAC-seq Guidelines

Since there are no ATAC-seq peaks of interest in the mitochondrial genome, these reads will only complicate the subsequent steps. Therefore, we recommend that they be removed from further analysis, via one of the following methods:

  1. Remove the mitochondrial genome from the reference genome before aligning the reads. In human/mouse genome builds, the mitochondrial genome is labeled ‘chrM’. That sequence can be deleted from the reference prior to building the genome indexes. The downside of this approach is that the alignment numbers will look much worse; all of the mitochondrial reads will count as unaligned.
  2. Remove the mitochondrial reads after alignment. A python script, creatively named removeChrom, is available in the ATAC-seq module to accomplish this.

Since the percentage of mtDNA-reads is a indicator of library quality, we usually remove mitochondrial reads after alignment. It is run as follows:

1
samtools view -@ $PPN -h ${sample}.bam | grep -v chrM | samtools sort -@ $PPN -O bam -o ${sample}.rmChrM.bam

PCR duplicates

Ref: Harvard FAS Informatics - ATAC-seq Guidelines

PCR duplicates are exact copies of DNA fragments that arise during PCR. Since they are artifacts of the library preparation procedure, they may interfere with the biological signal of interest. Therefore, they should be removed as part of the analysis pipeline.

One commonly used program for removing PCR duplicates is Picard’s MarkDuplicates.

1
2
3
4
5
${path2java} -XX:ParallelGCThreads=${PPN} -Djava.io.tmpdir=/tmp -jar ${path2picard} MarkDuplicates \
  QUIET=true INPUT=${sample}.bam OUTPUT=${sample}.marked.bam METRICS_FILE=${sample}.sorted.metrics \
  REMOVE_DUPLICATES=false CREATE_INDEX=true VALIDATION_STRINGENCY=LENIENT TMP_DIR=/tmp
# REMOVE_DUPLICATES=false: mark duplicate reads, not remove.
# Change it to true to remove duplicate reads.

MarkDuplicates will add a FALG 1024 to duplicate reads, we can remove them using samtools:

1
samtools view -h -b -F 1024 ${sample}.bam > ${sample}.rmDup.bam

Non-unique alignments

Ref: Harvard FAS Informatics - ATAC-seq Guidelines

Some researchers choose to remove non-uniquely aligned reads, using the -q parameter of samtools view.

Different genome aligners have varied implementation of mapping quality (MAPQ). See More madness with MAPQ scores (a.k.a. why bioinformaticians hate poor and incomplete software documentation). So, when using MAPQ to filter non-unique alignments, do check the MAPQ values of the aligner using.

For Bowtie2, people usually use MAPQ > 30.

1
2
# Remove multi-mapped reads (i.e. those with MAPQ < 30, using -q in SAMtools)
samtools view -h -q 30 ${sample}.bam > ${sample}.rmMulti.bam

Others

In the pipeline by ENCODE or some papers, the following reads were also removed (samtoolf flag 1796 or 1804).

  • reads unmapped,
  • not primary alignment
  • reads failing platform
  • duplicates

The remaining reads are so-called “properly mapped reads”.

1
2
3
# Remove reads unmapped, mate unmapped, not primary alignment, reads failing platform, duplicates (-F 1804)
# Retain properly paired reads -f 2
samtools view -h -b -F 1804 -f 2 ${sample}.bam > ${sample}.filtered.bam

Merging BAMs (optional)

When several libraries were constructed for one experimental condition (aka. one experimental condition inlcuded several biological and/or technical replicates), one may want to merge different BAM files before calling peaks (e.g. merge BAM files from technical replicates, merge BAM files to get bigger read depth).

Considerations about “merge BAMs” or “merge peaks” have been discussed:

  • ChIP-Seq: Calling peaks with replicates

    First, are these A) technical or B) biological replicates? That is, the same biological sample run several times with the same antibody (same lot also if polyclonal) protocol, or different biological samples run the same way with the same protocol?

    If it is A it may be reasonable to merge them for some analyses, such as just annotating peaks. I would merge the bam alignment files and then do the calls versus merging the calls.

    However, first you have analyze your replicates to check they they all perform the same. We did a lot of performance comparisons here: https://epigeneticsandchromatin.biomedcentral.com/articles/10.1186/s13072-016-0100-6

    You can steal those ideas, especially using the ENCODE segmentation tracks if it’s human and they have tracks for something like your cell type. But just counting the reads in bins and then doing a correlation is pretty informative.

    But even in our data, and we used a robot and do it a lot, one of our technical replicates behaved strangely. See supplemental figure S6.

    If it is B, biological replicates, you almost certainly don’t want to merge them. You will lose your information about biological variance is present. If you are looking at something like differential peaks between conditions DESeq and really all reputable programs will want some sort of replicates, almost always biological. In general, if you want to compute a p value on anything you need separate replicates (not merged).

    If you are just annotating peaks you don’t need a p value.

  • how to pool together biological replicates?

  • ChipSeq: merge bam file before peak calling

  • Chip-Seq merging peak files

And merging BAM can be done using samtools.

1
2
samtools merge -@ $PPN condition1.merged.bam sample1.bam sample2.bam sample3.bam
samtools index -@ $PPN condition1.merged.bam

Also, multiBamSummary in deepTools can be used to check the correlations between BAM files before merging.

Shifting reads

In the first ATAC-seq paper (Buenrostro et al., 2013), all reads aligning to the + strand were offset by +4 bp, and all reads aligning to the – strand were offset −5 bp, since Tn5 transposase has been shown to bind as a dimer and insert two adaptors separated by 9 bp (Adey et al., 2010).

Ref: shifting reads bam for NucleoATAC?

However, for peak calling, shifting of reads is not likely very important, as it is a pretty minor adjustment and peaks are 100s of basepairs. The shifting is only crucial when doing things where the exact position of the insertion matters at single base resolution, e.g. TF motif footprinting.

Also, remember that not all TF footprinting tools need shifted reads. Some of them may do this internally, e.g. NucleoATAC.

But, how to adjust the reads alignment?

First, we could do this using bedtools and awk.

Ref: Shifting reads for ATAC-seq alignments

1
2
3
4
5
6
# the BAM file should be sorted by read name beforehand
samtools sort -n -T aln.sorted -o aln.sorted.bam aln.bam

# The bedtools command should extract the paired-end alignments as bedpe format, then the awk command should shift the fragments as needed
bedtools bamtobed -i reads.bam -bedpe | awk -v OFS="\t" '{($9=="+"){print $1,$2+4,$6+4} \
  ($9=="-"){print $1,$2-5,$6-5}}' > fragments.bed

Or, we could do this using alignmentSieve.

1
2
3
4
5
6
7
# use --ATACshift
alignmentSieve --numberOfProcessors 8 --ATACshift --bam sample1.bam -o sample1.tmp.bam

# the bam file needs to be sorted again
samtools sort -@ 8 -O bam -o sample1.shifted.bam sample1.tmp.bam
samtools index -@ 8 sample1.shifted.bam
rm sample1.tmp.bam

We could also do this in R using ATACseqQC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
## load the library
library(ATACseqQC)

## input is bamFile
bamfile <- system.file("extdata", "GL1.bam", package="ATACseqQC", mustWork=TRUE)
bamfile.labels <- gsub(".bam", "", basename(bamfile))

## bamfile tags
tags <- c("AS", "XN", "XM", "XO", "XG", "NM", "MD", "YS", "YT")
## files will be output into outPath
outPath <- "splited"
dir.create(outPath)
## shift the bam file by the 5'ends
library(BSgenome.Hsapiens.UCSC.hg19)
seqlev <- "chr1" ## subsample data for quick run
which <- as(seqinfo(Hsapiens)[seqlev], "GRanges")
gal <- readBamFile(bamfile, tag=tags, which=which, asMates=TRUE)
gal1 <- shiftGAlignmentsList(gal)
shiftedBamfile <- file.path(outPath, "shifted.bam")
export(gal1, shiftedBamfile)

Peak calling using MACS2

Ref: Biostars - ATACseq with STAR and macs2

You typically use the --nomodel option, as the shifting model of MACS does not really make sense for open chromation data. As you have probably paired-end data, also use the -f BAMPE option. It forces MACS to pileup the real fragment length instead of an estimate, which maked sense imho, due to the quiet different fragment sizes that the library prep creates, also if you have paired-end why not make full use of it. Check reproducibility of the peaks between replicate samples, then rerun MACS with the merged bam file and feed the count matrix into DESeq2. Reference e.g. Corces et al 2016 Nat Genetics.

Ref: ATAC-seq settings · Issue #145 · taoliu/MACS

Liu Tao: If you followed original protocol for ATAC-Seq, you should get Paired-End reads. If so, I would suggest you just use --format BAMPE to let MACS2 pileup the whole fragments in general. But if you want to focus on looking for where the ‘cutting sites’ are, then --nomodel --shift -100 --extsize 200 should work.

Since paired-end sequencing is commonly used in ATAC-seq, so, we will tell MACS2 that the data is paired using the -f argument. By this way, MACS2 would only analyze properly mapped reads (as we get the bam after filtering above). The fragments are defined by the paired alignment, and there is no modeling or artificial extension.

1
2
3
4
# -f BAMPE, use paired-end information
# --keep-dup all, keep all duplicate reads.
macs2 callpeak -f BAMPE -g hs --keep-dup all --cutoff-analysis -n sample1 \
  -t sample1.shifted.bam --outdir macs2/sample1 2> macs2.log

Creating browser tracks

If -B parameter was used when running macs2 callpeak, you would get bedGraph files together with narrowPeak files. Someone would use these bedGraph files to create browser tracks (e.g. ParkerLab - ATAC-seq lab for BIOINF545), while others say they look kind of weird (Biostars - How to compare bigwig tracks of two ATAC libraries). I do not know yet.

I would like to create bigWig files for visualizing using bamCoverage in deepTools. It provides several different ways to normalize the signal.

1
2
3
4
# bam to bigwig, normalize using 1x effective genome size
# effective genome size: https://deeptools.readthedocs.io/en/latest/content/feature/effectiveGenomeSize.html
bamCoverage --numberOfProcessors 8 --binSize 10 --normalizeUsing RPGC \
  --effectiveGenomeSize $effect_genome_size --bam sample1.shifted.bam -o sample1.shifted.bw

Quality check

In processing ATAC-seq data, we would get several metrics to check the quality of data/libraries.

Ref:

Here is the standards used by ENCODE, and the detailed description of each term will be explained below.

Fragment/Insert size

Ref: Not A Rocket Scientist - ATAC-seq insert size plotting

One common QC for the data is to plot the fragment size density of your libraries. The successful construction of a ATAC library requires a proper pair of Tn5 transposase cutting events at the ends of DNA. In the nucleosome-free open chromatin regions, many molecules of Tn5 can kick in and chop the DNA into small pieces; around nucleosome-occupied regions, Tn5 can only access the linker regions. Therefore, in a normal ATAC-seq library, you should expect to see a sharp peak at the <100 bp region (open chromatin), and a peak at ~200bp region (mono-nucleosome), and other larger peaks (multi-nucleosomes). Examples from one of my data:

Regular scale:

Log scale:

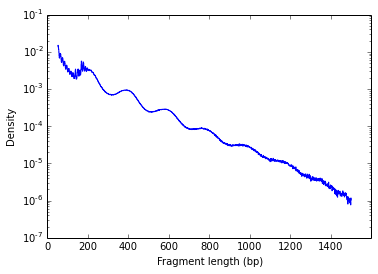
This clear nucleosome phasing pattern indicates a good quality of the experiment.

Different people probably have different way of plotting this using different codes, but making this plot can be simply achieved by a combination of one line of code and Excel. You don’t need some complicated scripts to do it at all.

samtools view ATAC_f2q30_sorted.bam | awk '$9>0' | cut -f 9 | sort | uniq -c | sort -b -k2,2n | sed -e 's/^[ \t]*//' > fragment_length_count.txt

See discussions here: Biostars - ATAC-seq fragment length distribution

%mitochondrial reads

High mitochondrial reads was a well-known problem, but in the latest ATAC-seq protocol (Omni-ATAC) this problem has been well addressed (Corces et al., 2017).

I guess in the future people will not care about this any more, and I keep this section in case.

Ref: Harvard FAS Informatics - ATAC-seq Guidelines

It is a well-known problem that ATAC-seq datasets usually contain a large percentage of reads that is derived from mitochondrial DNA (for example, see this discussion). Some have gone as far as using CRISPR to reduce mitochondrial contamination. The recently published Omni-ATAC method uses detergents to remove mitochondria and is likely to be more accessible for most researchers (but, do not follow their computational workflow).

The following code can be used to compute the percentage of mitochondrial reads.

Ref: Biostars - ATACseq alignment issues

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#!/bin/bash

#### Calculate percentage of reads mapped to mitochondrial genome (mtDNA) using SAMtools idxstats
#### Can be useful for ATAC-seq data. Requires an indexed BAM file:

if [[ $# -eq 0 ]] ; then
  echo '[ERROR]: No input file given!'
  exit 1
fi

## Check if index is present. If not, create it:
if [[ ! -e ${1}.bai ]];
  then
  echo '[INFO]: File does not seem to be indexed. Indexing now:'
  samtools index $i
  fi

## Calculate %mtDNA:
mtReads=$(samtools idxstats $1 | grep 'chrM' | cut -f 3)
totalReads=$(samtools idxstats $1 | awk '{SUM += $3} END {print SUM}')

echo '==> mtDNA Content:' $(bc <<< "scale=2;100*$mtReads/$totalReads")'%'

## Usage: ./script.sh atacseq.bam

Library complexity

Ref: ENCODE - ATAC-seq Data Standards and Prototype Processing Pipeline

Library complexity is measured using the Non-Redundant Fraction (NRF) and PCR Bottlenecking Coefficients 1 and 2, or PBC1 and PBC2. The preferred values are as follows: NRF>0.9, PBC1>0.9, and PBC2>3.

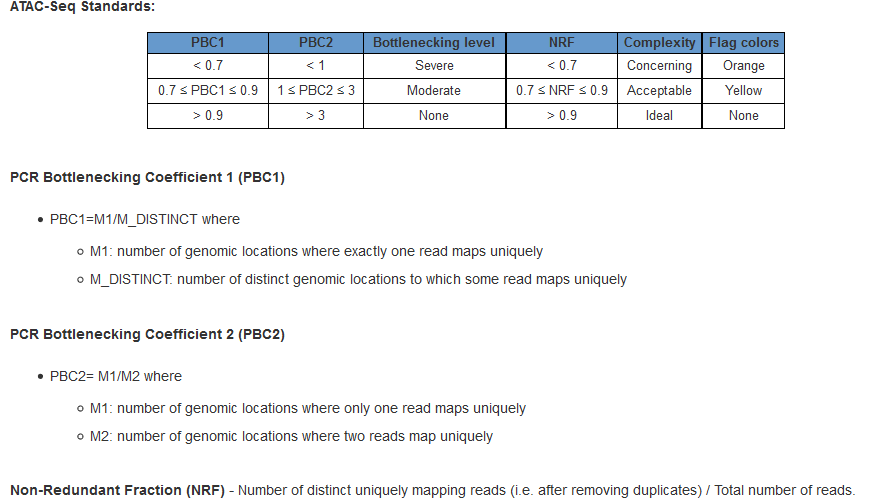
The following code was from ENCODE ATAC-seq pipeline.

1
2
3
4
5
6
7
8
9
10
# the bam used here is sorted bam after duplicates marking
# sort bam by names
samtools sort -@ 10 -n -O BAM -o tmp.bam ${sample}.bam

# calculate PBC metrics
bedtools bamtobed -bedpe -i tmp.bam | awk 'BEGIN{OFS="\t"}{print $1,$2,$4,$6,$9,$10}' \
  | grep -v 'chrM' | sort | uniq -c | awk 'BEGIN{mt=0;m0=0;m1=0;m2=0}($1==1){m1=m1+1} \
  ($1==2){m2=m2+1} {m0=m0+1} {mt=mt+$1} \
  END{printf "%d\t%d\t%d\t%d\t%f\t%f\t%f\n", mt,m0,m1,m2,m0/mt,m1/m0,m1/m2}' > ${sample}.pbc.qc
rm tmp.bam

Fraction of reads in peaks (FRiP)

Ref: ENCODE - Terms and Definitions

Fraction of reads in peaks (FRiP) - Fraction of all mapped reads that fall into the called peak regions, i.e. usable reads in significantly enriched peaks divided by all usable reads. In general, FRiP scores correlate positively with the number of regions. (Landt et al, Genome Research Sept. 2012, 22(9): 1813–1831)

Ref: Biostars - FRIP score ATAC-seq

In paired-end sequencing, we use the word fragment because the two reads that are produced always originate from the same DNA fragment and are therefore not independent of each other as reads from single-end sequencing would be. As FRiP comes from single-end ChIP-seq data, this is why they probably termed it reads. ATAC-seq is most commonly paired-end. You can use BEDtools for paired-end data but it requires more pre-processing of your data, that is why I use featureCounts, being faster and more convinient with plenty of customizable options. Choice is still yours. FRiP is probably not a very objective measure anyway, as it highly depends on how you prefilter your data, e.g. in terms of mapping quality, the definition of a properly-paired reads and the stringency of your peak calling (last sentence thinking aloud).

Ref: ENCODE - ATAC-seq Data Standards and Prototype Processing Pipeline

The fraction of reads in called peak regions (FRiP score) should be >0.3, though values greater than 0.2 are acceptable. For EN-TEx tissues (ENCODE GTEx tissue sample), FRiP scores will not be enforced as QC metric. TSS enrichment remains in place as a key signal to noise measure.

FRiP score can be calculated by samtools and bedtools:

1
2
3
4
5
6
7
8
9
10
# total reads
total_reads=$(samtools view -c ${sample}.bam)

# reads in peaks
reads_in_peaks=$(bedtools sort -i ${sample}_peaks.narrowPeak \
  | bedtools merge -i stdin | bedtools intersect -u -nonamecheck \
  -a ${sample}.bam -b stdin -ubam | samtools view -c)

# FRiP score
FRiP=$(awk "BEGIN {print "${reads_in_peaks}"/"${total_reads}"}")

While someone recommended to use featureCounts (https://www.biostars.org/p/337872/#337890), I found the results of featureCounts and intersectBed were close. So, I would like to use bedtools.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
samtools view -c ${sample}.bam
38439210

bedtools sort -i ${sample}_peaks.narrowPeak \
  | bedtools merge -i stdin | bedtools intersect -u -nonamecheck \
  -a ${sample}.bam -b stdin -ubam | samtools view -c
428359

awk 'BEGIN{FS=OFS="\t"; print "GeneID\tChr\tStart\tEnd\tStrand"} \
  {print $4, $1, $2+1, $3, "."}' ${sample}_peaks.narrowPeak > ${sample}_peaks.saf
featureCounts -p -a M0.A.005_peaks.saf -F SAF -o readCountInPeaks.txt ${sample}.bam
||    Total alignments : 19219605                                             ||
||    Successfully assigned alignments : 230826 (1.2%)                        ||

> 428359/38439210
[1] 0.0111438
> 230826/19219605
[1] 0.01200992

Find more details in note: Calculate FRiP score.

Transcription start site (TSS) enrichment

Ref: ENCODE - ATAC-seq Data Standards and Prototype Processing Pipeline

Transcription start site (TSS) enrichment values are dependent on the reference files used; cutoff values for high quality data are listed in the table below.

Ref: ENCODE - Terms and Definitions

Transcription Start Site (TSS) Enrichment Score - The TSS enrichment calculation is a signal to noise calculation. The reads around a reference set of TSSs are collected to form an aggregate distribution of reads centered on the TSSs and extending to 1000 bp in either direction (for a total of 2000bp). This distribution is then normalized by taking the average read depth in the 100 bps at each of the end flanks of the distribution (for a total of 200bp of averaged data) and calculating a fold change at each position over that average read depth. This means that the flanks should start at 1, and if there is high read signal at transcription start sites (highly open regions of the genome) there should be an increase in signal up to a peak in the middle. We take the signal value at the center of the distribution after this normalization as our TSS enrichment metric. Used to evaluate ATAC-seq.

The following code was from ATAqC.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
import numpy as np
import matplotlib
matplotlib.use('Agg')

import pybedtools
import metaseq
import logging

from matplotlib import pyplot as plt
from matplotlib import mlab

def make_tss_plot(bam_file, tss, prefix, chromsizes, read_len, bins=400, bp_edge=2000,
                  processes=8, greenleaf_norm=True):
    '''
    Take bootstraps, generate tss plots, and get a mean and
    standard deviation on the plot. Produces 2 plots. One is the
    aggregation plot alone, while the other also shows the signal
    at each TSS ordered by strength.
    '''
    logging.info('Generating tss plot...')
    tss_plot_file = '{0}_tss-enrich.pdf'.format(prefix)
    tss_plot_large_file = '{0}_large_tss-enrich.pdf'.format(prefix)

    # Load the TSS file
    tss = pybedtools.BedTool(tss)
    tss_ext = tss.slop(b=bp_edge, g=chromsizes)

    # Load the bam file
    bam = metaseq.genomic_signal(bam_file, 'bam') # Need to shift reads and just get ends, just load bed file?
    bam_array = bam.array(tss_ext, bins=bins, shift_width = -read_len/2, # Shift to center the read on the cut site
                          processes=processes, stranded=True)

    if greenleaf_norm:
        # Use enough bins to cover 100 bp on either end
        num_edge_bins = int(100/(2*bp_edge/bins))
        bin_means = bam_array.mean(axis=0)
        avg_noise = (sum(bin_means[:num_edge_bins]) +
                     sum(bin_means[-num_edge_bins:]))/(2*num_edge_bins)
        bam_array /= avg_noise
    else:
        bam_array /= bam.mapped_read_count() / 1e6

    # Generate a line plot
    fig = plt.figure()
    ax = fig.add_subplot(111)
    x = np.linspace(-bp_edge, bp_edge, bins)

    ax.plot(x, bam_array.mean(axis=0), color='r', label='Mean')
    ax.axvline(0, linestyle=':', color='k')

    # Note the middle high point (TSS)
    tss_point_val = max(bam_array.mean(axis=0))

    ax.set_xlabel('Distance from TSS (bp)')
    ax.set_ylabel('Average read coverage (per million mapped reads)')
    ax.legend(loc='best')

    fig.savefig(tss_plot_file)

    # Print a more complicated plot with lots of info

    # Find a safe upper percentile - we can't use X if the Xth percentile is 0
    upper_prct = 99
    if mlab.prctile(bam_array.ravel(), upper_prct) == 0.0:
        upper_prct = 100.0

    plt.rcParams['font.size'] = 8
    fig = metaseq.plotutils.imshow(bam_array,
                                   x=x,
                                   figsize=(5, 10),
                                   vmin=5, vmax=upper_prct, percentile=True,
                                   line_kwargs=dict(color='k', label='All'),
                                   fill_kwargs=dict(color='k', alpha=0.3),
                                   sort_by=bam_array.mean(axis=1))

    # And save the file
    fig.savefig(tss_plot_large_file)

    return tss_plot_file, tss_plot_large_file, tss_point_val

Blacklist filtering for peaks

One may want to filter peaks using DAC Blacklisted Regions.

The following code was from ENCODE - ATAC-seq Data Standards and Prototype Processing Pipeline

1
2
3
4
5
PEAK="${PREFIX}.narrowPeak"
FILTERED_PEAK="${PREFIX}.narrowPeak.filt.gz"
bedtools intersect -v -a ${PEAK} -b ${BLACKLIST} \
  | awk 'BEGIN{OFS="\t"} {if ($5>1000) $5=1000; print $0}' \
  | grep -P 'chr[0-9XY]+(?!_)' | gzip -nc > ${FILTERED_PEAK}

The 5th column of narroPeak file is integer score for display calculated as int(-10*log10qvalue). Since currently this value might be out of the [0-1000] range defined in UCSC Encode narrowPeak format, the awk code is to assign values greater than 1000 to 1000.

Merging peaks (optional)

One may want to merge peaks from different libraries or different samples.

Corces et al., 2016 used the following method to merge peaks, and I like their way:

To generate a non-redundant list of hematopoiesis- and cancer-related peaks, we first extended summits to 500-bp windows (±250 bp). We then ranked the 500-bp peaks by summit significance value (defined by MACS2) and chose a list of non-overlapping, maximally significant peaks.

We can do this by using BEDOPS (ref: Collapsing multiple BED files into a master list by signal)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#!/bin/bash

# modified from https://bedops.readthedocs.io/en/latest/content/usage-examples/master-list.html

summit_bed=(sample1_summits.bed sample2_summits.bed sample3_summits.bed)

out=fAdrenal.master.merge.bed

tmpd=/tmp/tmp$$
mkdir -p $tmpd

## First, union all the peaks together into a single file.
bedlist=""
for bed in ${beds[*]}
do
    bedlist="$bedlist $summit_bed"
done

# extended summits to 500-bp windows (±250 bp)
bedops --range 250 -u $bedlist > $tmpd/tmp.bed

## The master list is constructed iteratively.  For each pass through
## the loop, elements not yet in the master list are merged into
## non-overlapping intervals that span the union (this is just bedops
## -m).  Then for each merged interval, an original element of highest
## score within the interval is selected to go in the master list.
## Anything that overlaps the selected element is thrown out, and the
## process then repeats.
iters=1
solns=""
stop=0
while [ $stop == 0 ]
do
    echo "merge steps..."

    ## Condense the union into merged intervals. This klugey bit
    ## before and after the merging is because we don't want to merge
    ## regions that are simply adjacent but not overlapping
    bedops -m --range 0:-1 $tmpd/tmp.bed \
        | bedops -u --range 0:1 - \
        > $tmpd/tmpm.bed

    ## Grab the element with the highest score among all elements forming each interval.
    ## If multiple elements tie for the highest score, just grab one of them.
    ## Result is the current master list.  Probably don't need to sort, but do it anyway
    ## to be safe since we're not using --echo with bedmap call.
    bedmap --max-element $tmpd/tmpm.bed $tmpd/tmp.bed \
        | sort-bed - \
        > $tmpd/$iters.bed
    solns="$solns $tmpd/$iters.bed"
    echo "Adding `awk 'END { print NR }' $tmpd/$iters.bed` elements"

    ## Are there any elements that don't overlap the current master
    ## list?  If so, add those in, and repeat.  If not, we're done.
    bedops -n 1 $tmpd/tmp.bed $tmpd/$iters.bed \
       > $tmpd/tmp2.bed

    mv $tmpd/tmp2.bed $tmpd/tmp.bed

    if [ ! -s $tmpd/tmp.bed ]
    then
        stop=1
    fi

    ((iters++))
done

## final solution
bedops -u $solns \
   > $out

## Clean up
rm -r $tmpd

exit 0

Outreach

Well, then we complete the main upstream ATAC-seq data analysis. For downstream analysis, one may want to annotate peaks, find enriched motifs of TFs, compare peaks under different conditions and combine ATAC-seq data with other data types like RNA-seq etc.

Change log

  • 20190103: create the note.
  • 20190320: complete the note.
  • 20190401: update the section of “Merging BAMs”. Add some discussions about “pooling replicates”
0%